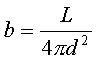MVNSC: Mississippi Valley Night Sky Conservation:
The Night Sky Around Us Lecture 5
Program developed by:
- Mississippi Valley Conservation Authority
- Royal Astronomical Society of Canada
- Ottawa Astronomy Friends
- Instructor: Pat Browne
- Assistants: Shawn McKay, Bob Hillier
- Note: Donations can be receipted as charitable . Donations can be made online at canadaHelps – Mississippi Valley Conservation (choose Night Sky Conservation fund)
May 1 2015 – Quick Observing Report – Starlight Observations
We went to FLO and observed with the 16″ F5 Reflector Telescope
- Eyepiece: 6mm ortho (300x)
- Rainbow Optics Diffraction Grating
- Viewport Lens to widen colour bands
We aligned on the brightest object in the Winter Sky – Sirius in Canis Major
- Setting rapidly
- Color distorted by atmospheric reddening and scintillation
Starlight observation: Due to the low altitude of this star we did not see indication of spectral class – type A (white)
- Shorter wavelengths (blue) are more likely to be scattered by the air molecules and the small particles, and so by the time the light has passed through the atmosphere, the longer wavelengths dominate. This resulting light we perceive as red. See:
Rainbows and Atmospheric Effects
The star, a white class A (A1) hydrogen-fusing dwarf(main sequence star) with a temperature of 9880 Kelvin, is bright
- because it is rather luminous, 26 times more so than the Sun
- but mostly because it is nearby, a mere 8.6 light years away, just double that of the closest star to the Earth (Alpha Centauri)
Venus Spectrum is nice and bright and mimics the Sun:
Venus’ atmosphere is completely cloud covered. Since Venus is an inner planet, it never strays far from the Sun. Since Venus is also very bright, it serves as a marker to find other planets if they are directly near our line of sight: See: https://millstonenews.com/2015/01/finding-planet-mercury-january-2015-with-a-little-help-from-venus.html
Planet Jupiter and observed the moons Io, Europa, Ganymede, Callisto
According to calculations in computer programs, stellarium and StarMap, we should have started with three moons 9:57pm Local time 
Then by 10pm we should have seen all 4 moons, with Europa emerging from behind Jupiter. The second snapshot from stellarium is 9:59pm local time
Using software to help identify and understand your observations
Stellarium is a night sky viewing program that you can use to help identify what you saw at your location at a particular time. We are fortunate to be able to confirm our observations – or recognize we have to re-do them for consistent results or to improve your observation. This was the case with the Jovian moons.
Padua, Italy 1610: Imagine a large room with a high ceiling, a desk and a chair. Seated in the chair is a middle-aged man named Galileo Galilei, one of the most prominent scientists of his time. He has just spent two nights observing the planet Jupiter with a small telescope This is the first time a telescope has ever been used to look at the night sky. Still not believing his on observations, he is completing his notes on the four moons he has discovered, four moons that revolve about Jupiter and not the Earth..."
More Things in Heaven and Earth, Poets and Astronomers Read the Night Sky by David Levy
Our moon was nearly full, another case where it’s hard to know what feature we’re looking at. The trick is to go towards the edge of the moon (there is no limb of shadow relief!). We probably saw:
image courtesy Virtual Moon
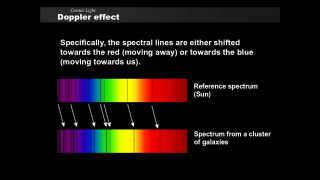
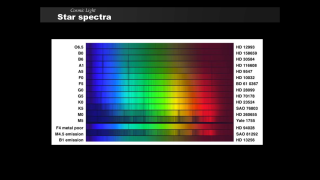
Now that we have seen how starlight spectra provide markers for
- temperature and state of nuclear fusion processes
- chemical composition
- Spectral shifts are indicators of relative velocity – application: Spectroscopic Binaries, line of sight velocities to stars, clusters and even galaxies…
Higher frequency waves towards us, lower frequency waves away from us (red shift) - stellar classification in terms of O B A G K M
Starlight Luminousity – How bright is your star
At the Mill of Kintail we can gauge naked eye magnitude as roughly “mag 5”. In the city, only the brightest stars shine brighter than the light pollution mag 2 or 3.
Brightness of Distant Celestial Objects
The brightness or Luminousity of the star, star cluster or galaxy is the measure of the Source of radiation Energy: Luminosity is usually measured in watts or as a multiple of the Sun’s luminosity (Luminousity of the Sun(Joules/Sec) = 3.90 x 1026 W)
As the radiant energy leaves the object it spreads outwards in a sphere of increasing radius. The energy passing through each square metre on the surface of the sphere per second is found by dividing the luminosity of the star, L, by the sphere’s surface area
Therefore The Light from the Star Falls Off as the Square of the Distance
Why stars are brighter or fainter – Distance or Luminousity?
A star might be brighter than another star because:
- It is extremely energetic and its stellar properties produce intense visible radiation. In this case the objects intrinsic brightness or luminousity dominates. If we know the star’s intrinsic luminousity, we can determine its distance
- It is at a closer distance to our solar system
By comparing:
- this intrinsic brightness known as Absolute Magnitude M
…to…
- the visual (observed magnitude m ) we can determine the star’s distance.
- We arrive at the Distance modulus – Difference in M-m => Distance
These stars with known absolute Magnitudes are special stars used for calibration of the distance ladder. Typically these are stars on the Main Sequence:
Distances to the Stars, Star Clusters and Galaxies
Astronomers speak of a distance ladder. Each rung gives a ‘leg-up’ to the next method of distance determination. The first method of measurement is direct; the rest use indirect methods calibrated using a ‘standard candle’, something that you know is a certain absolute luminosity (magnitude) and hence determine its distance by measuring its absolute magnitude and comparing it to its apparent magnitude
Direct Measurement to Nearby Stars using Stellar Parallax (Satellite Hipparcos data)
The KEY to going from Direct Measurements such as trigonometric parallax for nearby stars, to indirect measurements, is we calibrate the indirect measure of Absolute Magnitude using parallax. We can calibrate the relative magnitude observed (even visually) to the Absolute magnitude derived scientifically and get the true brightness and distance modulus for that star.
Absolute Magnitude: Absolute magnitude is the measure of a celestial object’s intrinsic brightness. It is the the same as the visual magnitude of a star when it is placed at a distance of 10.0 parsecs or about 32.6 light years from the observer
So according to this definition we compare magnitudes between stars that we know at a given distance to stars of unknown magnitude. …
The absolute magnitude of a star, M is the magnitude the star would have if it was placed at a distance of 10 parsecs from Earth. By considering stars at a fixed distance, astronomers can compare the real (intrinsic) brightness of different stars. This means that all stars at a distance of 10 parsecs or roughly 32.6 (like Arcturus) light years (measured using the direct method of trigonometric parallax !) have an absolute magnitude equal to their apparent magnitude.
To convert the observed brightness of a star (the apparent magnitude, m) to an absolute magnitude, we need to know the distance, d, to the star. Alternatively, if we know the distance and the apparent magnitude (m) of a star, we can calculate its absolute magnitude M.
Examples:
Difference: M-m tells us the Distance Modulus
Sometimes we know the direct distances to stars based on trigonometric parallax
Therefore we can determine the absolute magnitude.
When m = M, we have a calibration of a star's intrinsic brightness.
Arcturus: Absolute Magnitude M:-0.30
Apparent Magnitude m:-2.25
M-m = 2 Distance is roughly 25 pc
Vega: Absolute Magnitude: 0.58
Apparent Magnitude: 0.03
M-m = 1 Distance from the table is < 10 pc
Distances derived from formula: starting with difference of magnitudes of 2.5 relating to the inverse square of distance:
Distance Modulus: M-m = 2.5 *log(d/10)^2
= 5 * (log(d) - log(10))
= 5 * (log(d) -1)
= 5 * log(d) -5
log(d) = (M-m + 5)/5
d = 10^((M-m + 5)/5)
Main Sequence Stars can be measured
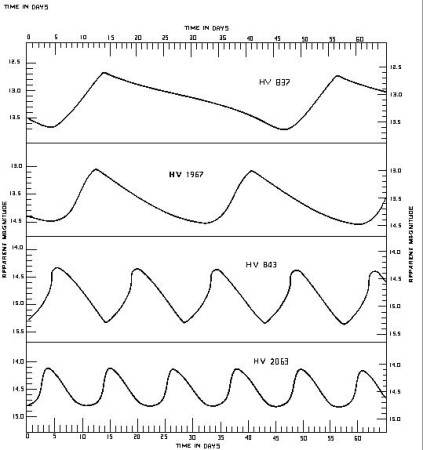
Here is Mary Lou Whitehorne’s hand-made graph of the Brightest stars – mostly along the Main Sequence. She was curious to determine her own value for one of her favouate Variable Stars in Perseus.
Here are her calculations based on the M-m values that she picked off her graph
Main Sequence Fitting for Star Clusters – Open Cluster Example
We use the known absolute magnitude of a well-known star cluster to determine that of the unknown cluster.
- Astronomers take images of the cluster through special Blue and Visual filters to determine the apparent magnitudes very accurately.
- The difference between the Apparent and the Absolute magnitudes gives the distance to the cluster.
In this example, we measure a difference in the two clusters of 5.5…
Average distance for the cluster: m - M = 5.5 Average distance to the cluster = 10 ^((5.5 + 5)/5 = 10^2.1 = 126 pc
Because… Distance Modulus: m – M = 5*log(d/10)
(m-M) = 5 *(log(d) - log(10) m - M = 5*log(d) - 5*1 ( m - M + 5 ) / 5 = log (d) Distance in parsecs: d = 10 ^ (m - M + 5 )/5 (parsecs or pc)
Graphing Periodic Variation in Brightness – Cepheid Variable Stars in other clusters
Variable Stars Periodic Variations in their brightness lead to a calibration of values of Absolute Magnitude of special stars in the cluster .
Variable Stars – Henrietta Leavitt: Period-Luminosity Relationship
Watch how Henrietta discovered using Cepheid Variables the true, absolute brightness of these special ‘standard candles’
See: https://millstonenews.com/wp-content/uploads/2015/05/Cepheid-Variables-1-1.mp4
- Calibrating the Main Sequence:
Period-Luminousity Graph for Cepheid Variables in Star Clusters
For Cepheid Variables , Henrietta determined the Period-Luminosity Relationship which calibrates the Absolute Magnitude Scale:
Re-Searching the Stars…
We have seen…observations and recording techniques. Carefully studying the stars, finding that for Cepheid Variables, the longer the period, the higher the intrinsic luminuousity provides stellar distance calibration. When we observe these objects, we can determine how far and therefore how long ago the light left that source.
Observing Plan – Early Spring within and Beyond the Galaxy From Pairs of Stars to Pairs of Galaxies.
To learn to be a good observer, we use the following guidelines: https://millstonenews.com/2014/04/night-sky-observing-tips.html
For our Observing Exercise, we will use https://millstonenews.com/2014/03/early-spring-night-sky-observing.html
